728x90
반응형
크루스칼 알고리즘 (Kruskal)
- 그리디 알고리즘
: 그 순간에 최적이라고 생각되는 것을 선택
- 시간복잡도 : e log e
- 과정
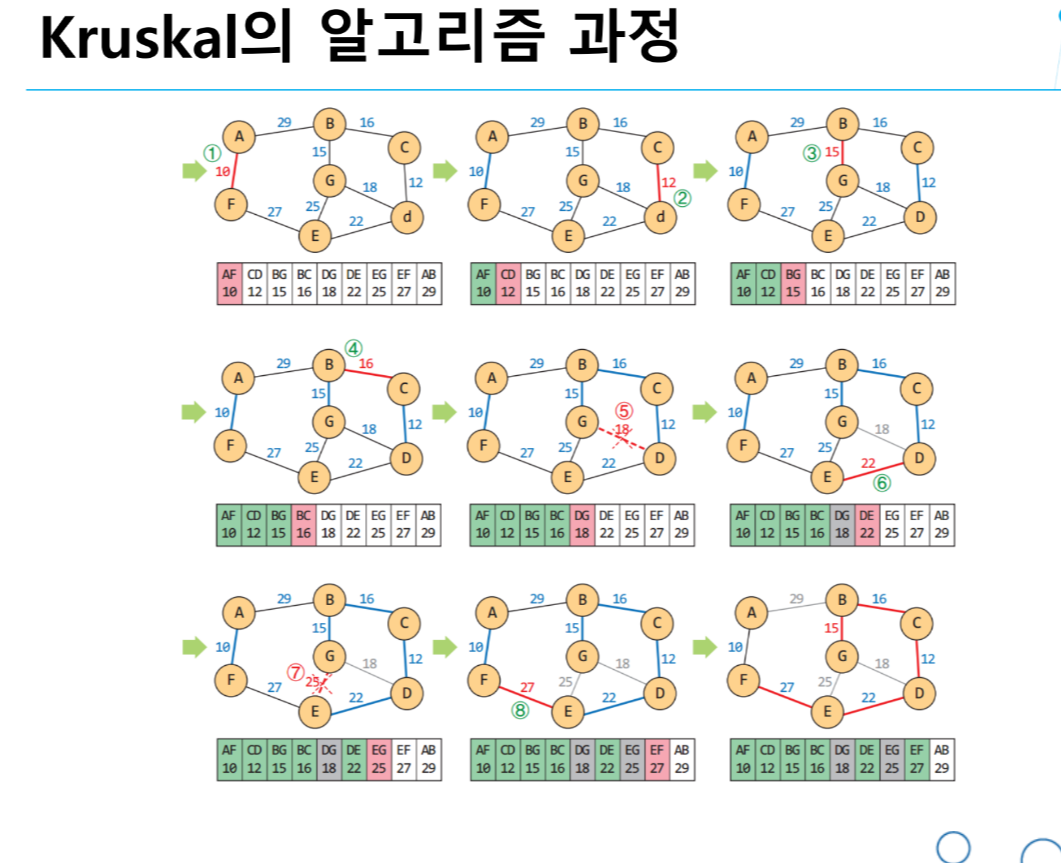
1> 그래프의 모든 간선을 가중치에 따라 오름차순으로 정렬한다.
2> 가장 가중치가 작은 간선 e를 뽑느다.
3> e를 신장트리에 넣었을 때 사이클이 생기면 넣지 않고 2번으로 이동한다.
4> 사이클이 생기지 않으면 최소 신장 트리에 삽입한다.
5> n-1개의 간선이 삽입될 때 까지 2번으로 이동한다.
- union-find 알고리즘을 활용
> union : 두 집합의 합집합을 만드는 연산
> find: 원소가 속한 집합을 찾는 연산
=> 대표값을 비교함으로써 순환구조 판단
ex)

코드
# union-find
parent =[] # 각 노드의 부모노드 인덱스
set_size=0 # 전체 집합의 개수
def init_set(nSets): # 집합의 초기화 함수
global set_size,parent # 전역변수 사용을 위함
set_size = nSets # 집합의 개수
for i in range(nSets): # 모든 집합에 대해
parent.append(-1) # 각각이 고유의 집합(부모가 -1)
def find(id): # 정점 id가 속한 집합의 대표번호 탐색
while parent[id]>=0: # 부모가 있는 동안 (-1이 아닌 동안)
id=parent[id] # id를 부모 id로 갱신
return id # 최종 id 반환. 트리의 맨 위 노드의 id임
def union(s1,s2): # 두 집합을 병합(s1을 s2에 병합시킴)
global set_size # 전역변수 사용을 위함
parent[s1] = s2 # s1을 s2에 병합시킴
set_size = set_size - 1 # 집합의 개수가 줄어듦
# Kruskal
def MSTKruskal(vertex,adj): # 매개변수: 정점리스트, 인접행렬
vsize=len(vertex) # 정점의 개수
init_set(vsize) # 정점 집합 초기화
eList =[] # 간선 리스트
for i in range(vsize-1): # 모든 간선을 리스트에 넣음
for j in range(i+1,vsize):
if adj[i][j] != None:
eList.append((i,j,adj[i][j])) # 튜플로 저장
eList.sort(key=lambda e: e[2], reverse=True) # 간선 리스트를 가중치의 내림차순으로 정렬: 람다 함수 사용
edgeAccepted = 0
while edgeAccepted < vsize-1: # 정점 수 - 1 개의 간선
e = eList.pop(-1) # 가장 작은 가중치를 가진 간선
uset = find(e[0]) # 두 정점이 속한 집합 번호
vset = find(e[1])
if uset != vset: # 두 정점이 다른 집합의 원소라면
print("간선 추가 : (%s,%s,%d)"%(vertex[e[0]],vertex[e[1]],e[2])) # 간선추가 출력
union(uset,vset) # 두 집합을 합함
edgeAccepted +=1 # 간선이 하나 추가됨
# 테스트 코드
vertex = ['A','B','C','D','E','F','G']
weight =[
[None,29,None,None,None,10,None],
[29,None,16,None,None,None,15],
[None,16,None,12,None,None,None],
[None,None,12,None,22,None,18],
[None,None,None,22,None,27,25],
[10,None,None,None,27,None,None],
[None,15,None,18,25,None,None]
]
MSTKruskal(vertex,weight)728x90
반응형